Pulsierender Flüssigkeitszerfall
© Zoltán Faragó, 1996
Traditionelle Vorstellung zum Zerfall eines runden Flüssigkeitstrahles in einem koaxialen Gasstrom.
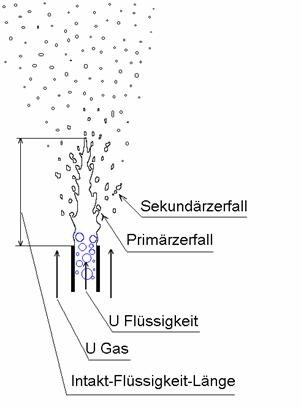
Mayer, W.O.H.: Zur koaxialen Flüssigkeitszerstäubung im Hinblick auf die Treibstoffaufbereitung in Raketentriebwerken, DLR-FB 93-09, Lampoldshausen, 1993
|
|
Experiments in Fluids
Publisher: Springer-Verlag Heidelberg ISSN: 0723-4864 (Paper) 1432-1114 (Online) DOI: 10.1007/s00348-003-0675-0 Issue: Volume 36, Number 4 Date: April 2004 Pages: 528 - 539 |
|
Atomization characteristics on the surface of a round liquid jet W. O. H. Mayer |
M. VARGA†, J. C. LASHERAS AND E. J. HOPFINGER:
Initial breakup of a small-diameter liquid jet by a high-speed gas stream
J. Fluid Mech. (2003), vol. 497, pp. 405–434. c _ 2003
Hypothese des pulsierenden Flüssigkeitsstrahl-Zerfalles.
Im Gegensatz zu den oben angedeuteten statischen Modellen erfolgt der Flüssigkeitszerfall durch eine Reihe pulsierender Vorgänge. Der freie Flüssigkeitsstrahl befindet sich in einem instabilen Gleichgewichtzustand. Nach durchlaufen verschiedener Instabilitäten (Kelvin-Helmholz-, Plateau-Rayleigh- oder Taylor-Instabilität) wird der intakte Flüssigkeitsstrahl zum Spray. Eine der wichtigsten treibenden Kräfte ist dabei die Minimierung der Oberfläche (Plateau, 1849). Die durchlaufenen Instabilitäten führen zu oszillierenden Vorgängen bei der Zerstäubung. In diesem Essay werden Pulsierungen beim Zerfall des runden Strahles, des ebenen und des rotierenden Flüssigkeitsfilmes aufskizziert.
Beim Fiber-Zerfall des runden Flüssigkeitsstrahles mittels eines Koaxialzerstäubers können wenigstens drei pulsierend ablaufende Schritte beobachtet werden.
1 Der Zerfall der einzelnen Fiber nach dem von zuerst von Plateau (1849)
beschriebenen Mechanismus, der in der Literatur meist als Rayleigh-Zerfall (1878) bezeichnet wird. Die charakteristische Zerfallszeit beträgt:
Δt1 = (4,5∙DFiber) / Δu mit
DFiber : Fiber-Durchmesser und
Δu1 : Längen-Wachstumsgeschwindigkeit der Fiber
Zerfallfrequenz = 1 / Δt1
2 Bildung der einzelnen Fiber. Die charakteristische Fiberbildungszeit beträgt:
Δt2 = (LFA) / Δu2 mit
LFA : Fiberabstand
Δu2 : Oberflächengeschwindigkeit des Flüssigkeitsstrahles
Fiberbildungsfrequenz = 1 / Δt2
3 Bildung von großen Flüssigkeitsstrukturen. Die charakteristische Bildungszeit beträgt:
Δt3 = (Li.L.,max - Li.L.,min ) / Δu3 oder ΔLL / Δu4 mit
Li.L., max : maximale intakte Flüssigkeitslänge
Li.L., min : minimale intakte Flüssigkeitslänge
ΔLL : Großstrukturabstand
Δu3 : Kolbengeschwindigkeit des Flüssigkeitsstrahles
Δu4 : Großstrukturgeschwindigkeit
Frequenz der Großstrukturbildung = 1 / Δt3
Die dritte Pulsierungsart ist die wichtigste beim Zerfall eines koaxialen Flüssigkeitsstrahles. Wesentlichen Merkmale dieser Pulsierung sind die Schwankung der intakten Länge
Li.L., max > Li.L > Li.L., min
und die Schwankung des spezifischen Massenstromes an der Sprayachse
> 
> 
.
Die Pulsierungsfrequenz kann bei Verbrennungsvorgängen zu Verbrennungsinstabilitäten führen, insbesondere, wenn die Pulsierungsfrequenz mit einer der akustischen Eigenfrequenzen des Verbrennungsraumes übereinstimmt.
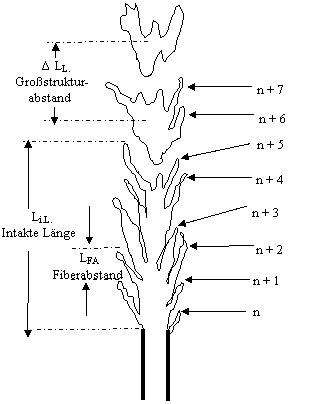
Fiberzerfall und Super-Pulsierender Zerfall:
Faragó, Zoltán und Chigier, Norman: Parametric Experiments on Coaxial Airblast Jet Atomization, ASME Gas Turbine and Aeroengine Congress, ASME 90-GT-81, Brussels, Belgium, 1990
Faragó, Z. und Chigier, N.: Morphological Classification of Disintegration of Round Liquid Jets in a Coaxial Air Stream, Atomisation and Sprays, Vol. 2, pp. 137-157, 1992
Frequenz der Großstrukturpulsierung = (Großstrukturabstand / Großstrukturgeschwindigkeit)
Für laminare Flüssigkeitsströmung bei geringer Geschwindigkeitsdifferenz zwischen Flüssigkeit und Gas beträgt die Frequenz der Großstrukturpulsierung:
mit
als
Austrittsgeschwindigkeit der Flüssigkeit und
als Durchmesser des
Flüssigkeitsstrahles.
Für turbulente Flüssigkeitsströmung bei geringer Geschwindigkeitsdifferenz zwischen Flüssigkeit und Gas beträgt die Pulsierungsfrequenz:
.
Die Pulsierungsfrequenz erhöht sich mit zunehmender Geschwindigkeitsdifferenz zwischen Flüssigkeit- und Gasstrom.
|
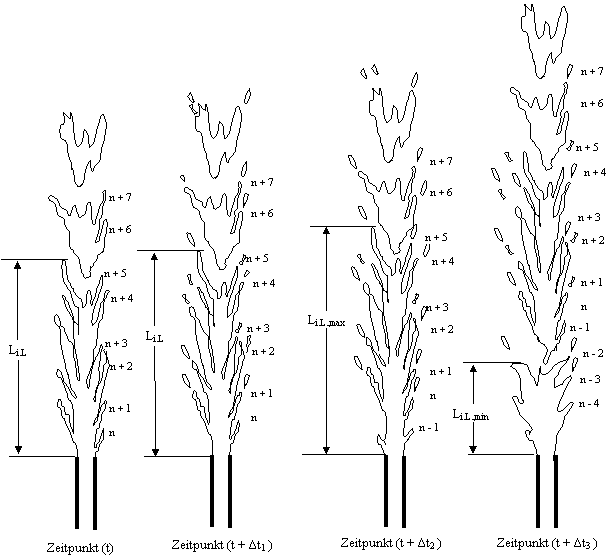
Authors: |
|
Eroglu, Hasan; Chigier, Norman; Faragó, Zoltán: Coaxial atomizer liquid intact lengths |
|
Affiliation: |
|
AA (Carnegie-Mellon University, Pittsburgh, PA), AB (Carnegie-Mellon University, Pittsburgh, PA), AC (DLR, Institut für Chemische Antriebe und Verfahrenstechnik, Hardthausen am Kocher, Federal Republic of Germany) |
|
Journal: |
|
Physics of Fluids A (ISSN 0899-8213), vol. 3, Feb. 1991, p. 303-308. Research supported by NASA. |
P. MARMOTTANT AND E. VILLERMAUX : On spray formation ;
J. Fluid Mech. (2004), vol. 498, pp. 73–111
(achsialsymmetrischer) Plateau-(Rayleigh)-Zerfall
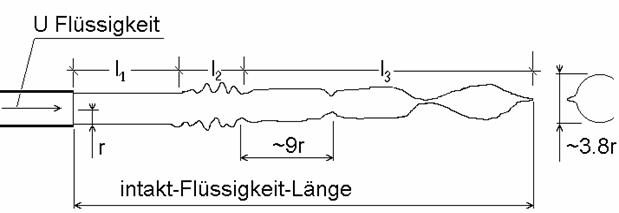
J. Plateau, Statique Experimentale et Theorique des Liquides Soumis aux Seules Forces Moleculaires (Gaitier-Villars, Paris, 1873); Acad. Sci. Bruxelles M. 23, 5 (1849).
Lord Rayleigh: On the Instability of Jets, Proc. London Math. Soc., Bd. 10, pp 4-10, 1878
Einfluss der Oberfläche auf den Flüssigkeitwsdruck
Der Flüssigkeitsdruck in einem zylindrischen Strahl, verursacht durch die Oberflächenspannung s:
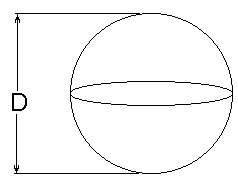
Der Flüssigkeitsdruck in einem sphärischen Tropfen, verursacht durch die Oberflächenspannung s:
Kraft: F= Dps, Fläche: A=D2 p/4, Druck: p = F/A = Dps / (D2 p/4) = 4s/D
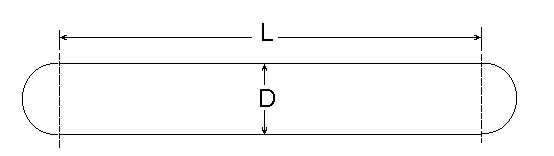
p=4s/D p =2s/D
 |
|
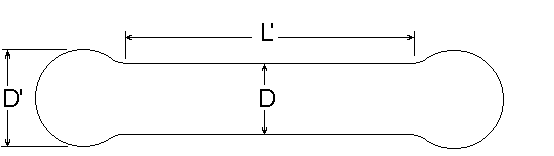
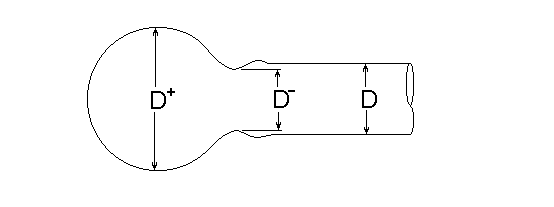
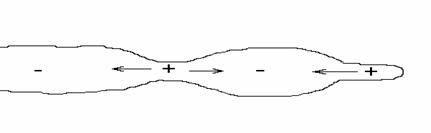
Deformation durch Druckdifferenzen im Flüssigkeitsstrahl beim Plateau-Rayleigh-Zerfall
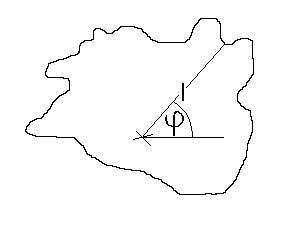
Berechnung des Wandabstandes nach dem Buleev’schen turbulenten Austauschmodell:
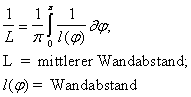
Buleev, N. , Timukhina, M.: Simplified Formulas for the Turbulent Exchange Coefficients in Fluid Flow; High Temperature, Vol. 7, (1969), pp. 96 ff.
Buleev, N., Polosukhina, K., Pyshin, V.: Hydraulic Resistance and Heat Transfer in a Turbulent Liquid Stram; High Temperature, Vol. 2 (1964), pp. 673 ff.
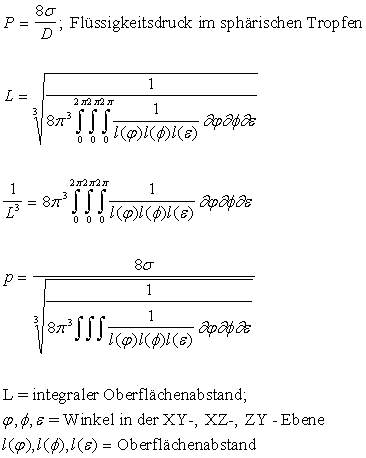
Beispiele verschiedener Zerfallsmodi
unsymmetrischer Plateau-(Rayleigh)-Zerfall nach Faragó und Chigier
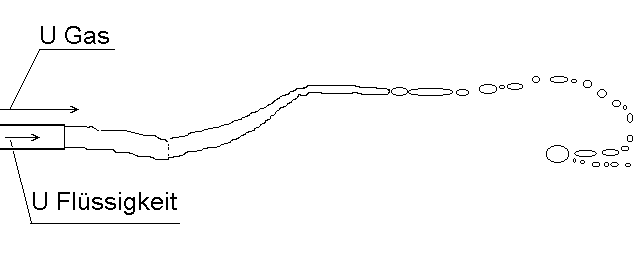
Faragó, Z. und Chigier, N.: Parametric Experiments on Coaxial Airblast Jet Atomization, ASME Gas Turbine and Aeroengine Congress, ASME 90-GT-81, Brussels, Belgium, 1990
Faragó, Z. und Chigier, N.: Morphological Classification of Disintegration of Round Liquid Jets in a Coaxial Air Stream, Atomisation and Sprays, Vol. 2, pp. 137-157, 1992
Memebran-Zerfall eines runden Wasserstrahles nach Faragó und Chigier
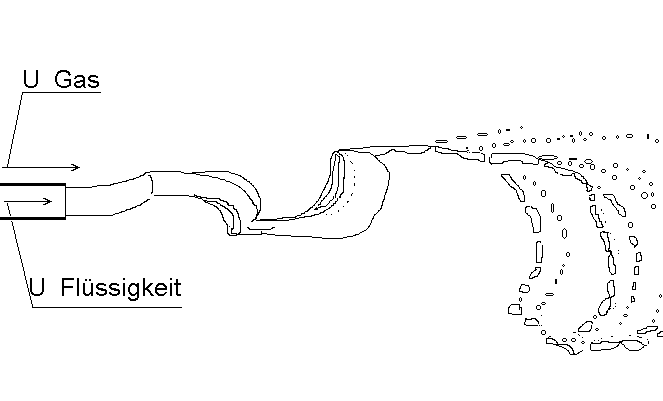
Faragó, Z. und Chigier, N.: Parametric Experiments on Coaxial Airblast Jet Atomization, ASME Gas Turbine and Aeroengine Congress, ASME 90-GT-81, Brussels, Belgium, 1990
Faragó, Z. und Chigier, N.: Morphological Classification of Disintegration of Round Liquid Jets in a Coaxial Air Stream, Atomisation and Sprays, Vol. 2, pp. 137-157, 1992
Film-Zerfall nach Fraser et al.
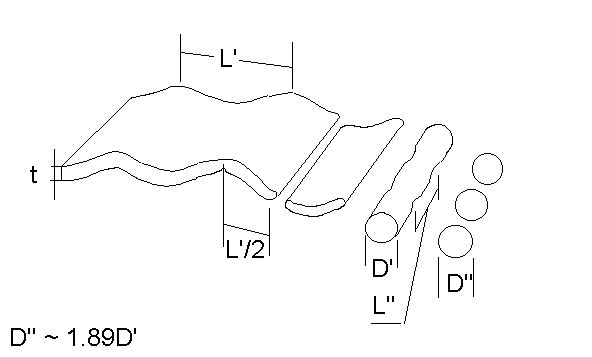
Fraser, R.P., Eisenklam, P., Dombrowski, N. und Hasson, D.: Drop Formation from Rapidly Mooving Sheets, AIChE J., Vol. 8, No 5, 1962, pp. 672-680
Dombrowski, N., and Johns, W.R.: The Aerodynamic Instability and Disintegration of Viscous Liquid Sheets, Chem. Eng. Sci., Vol. 18, 1963, pp. 203-214
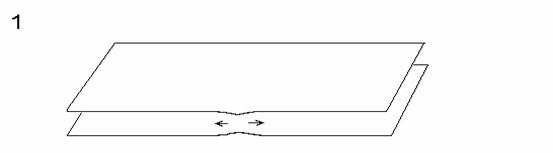
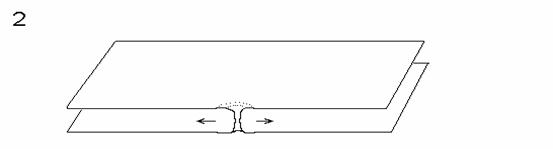
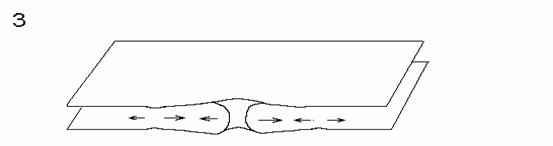
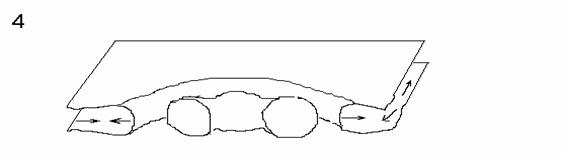
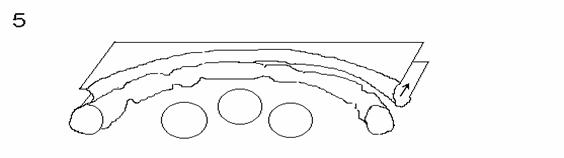
Film-Zerfall durch druckinduzierte Rißbildung (Bild 1-3) und durch Wulstbildung am Filmrand (Bild 4-5)
Zerfall des rotierenden Filmkegels einer Druckdralldüse durch Taylor-Wirbel
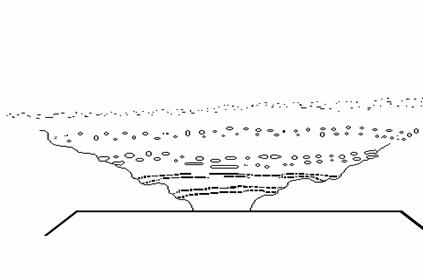
Taylor-Wirbel
 |
Faragó, Z. und Bendix, D.: Investigation on evaporating sprays; Partec’95, 11th ILASS-Europe Conference on Atomization and Sprays, Nürnberg, 1995
Bendix D.: Untersuchung und Bewertung von Dralldüsen für Heizölbrenner kleiner Leistung, Diplomarbeit, Martin-Luther-Universität, Halle-Wittenberg, 1994
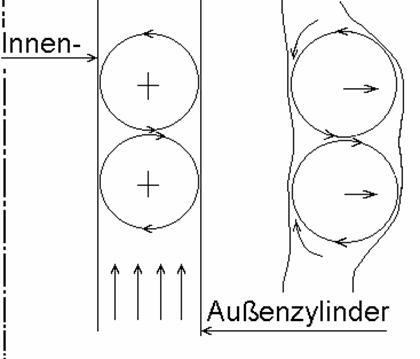
Links: Taylor, G.I.: Stability of viscous liquid contained between two rotating cylinders; Phil. Trans. Roy. Soc. A 223, 1923, 289
Rechts: Faragó, Z.: Kraftstoffaufbereitung und Verbrennung in Brennern, Wehrtechnisches Symposium: Kraftstoffe; Bundesakademie für Wehrverwaltung und Wehrtechnik, Mannheim, 1985
Bedingung zur Entstehung des Taylor-Wirbels
Prinzipskizze des Zerfalls des rotierenden Filmkegels durch Taylor-Wirbel
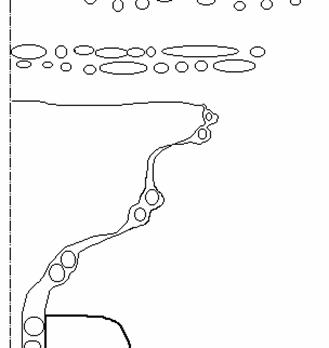
Zerfall des rotierenden Filmkegels einer Druckdralldüse durch Wulstbildung am Kegel-Ende
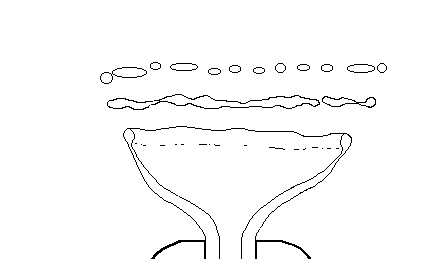
Bayvel, L., Orzechowski, Z.: Liquid Atomization, Taylor and Francis, 1993
Pulsierung beim Zerstäuben mittels Druckdralldüse
D0 : Durchmesser der Düsenaustrittsbohrung
Dmax : Durchmesser des grüßten Tropfens im Spray
L: Länge des intakten Flüssigkeitsfilmes
: Niedrigster
Düsenmassenstrom, bei dem sich ein Luftkern in der Dralldüse bildet
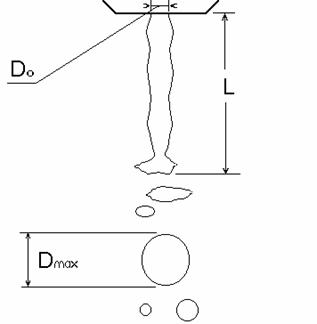
Dmax/ D0
» 2 - 4; L/ D0 » 5 - 10 » 0.7
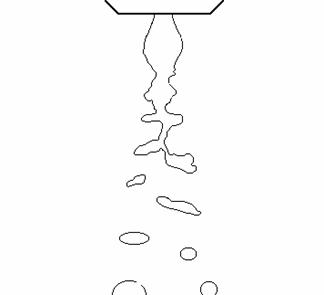
Dmax / D0
» 2 - 3; L/ D0 » 8 - 12 » 0.9 - 1
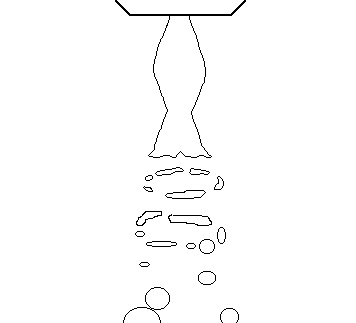
Dmax / D0
» 1.5 - 3; L/ D0 » 8 - 12 » 1 - 1.1
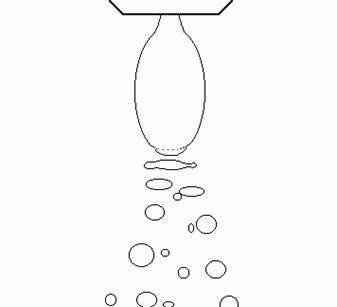
Dmax / D0
» 1.5 - 3; L/ D0 » 10 - 15 » 1.5
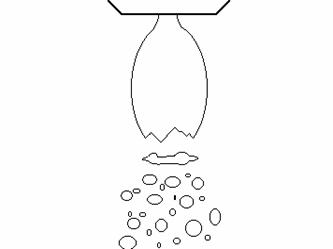
Dmax / D0
» 1 - 2; L/ D0 » 12 - 20 » 1.7
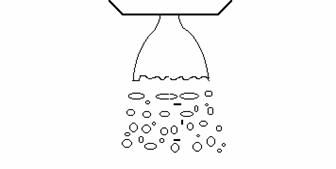
Dmax / D0 » 0.6 - 1.5; L/ D0 » 6 - 12 » 2
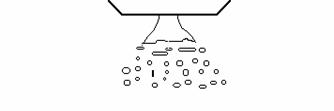
Dmax / D0
» 0.3 - 1; L/ D0
» 2 - 8 > 2.5
Zerfallkategorisierungen
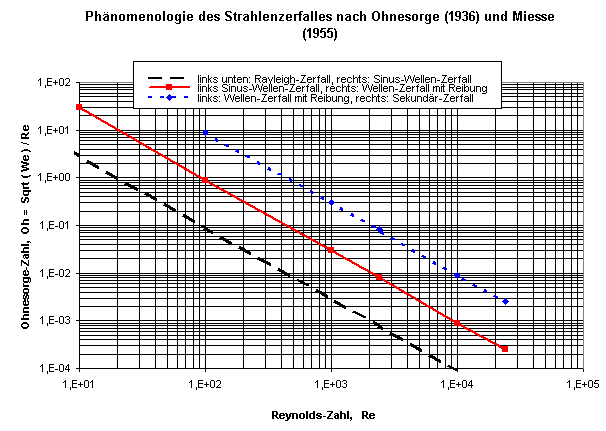
Ohnesorge, W.: Die Bildung von Tropfen aus Düsen beim Zerfall flüssiger Strahlen ( Formation of Drops by Nozzles and the Disruption of the Breakup of Liquid Jets), Z. Angew. Math. Mech., Vol 16, 1936, pp. 355-358
Miesse, C.C.: Correlation of Experimental Data on the Disintegration of Liquid Jets, Ind. Eng. Chem., Vol. 49, No. 9, 1955
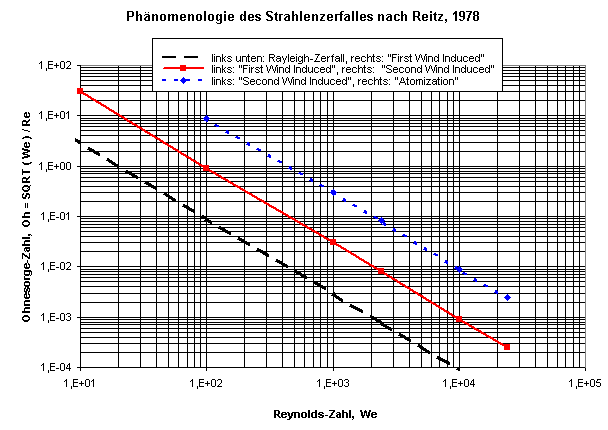
Reitz, R. D.: Atomization and Other Breakup Regimes of a Liquid Jet, Ph.D. thesis, Princeton University, 1978
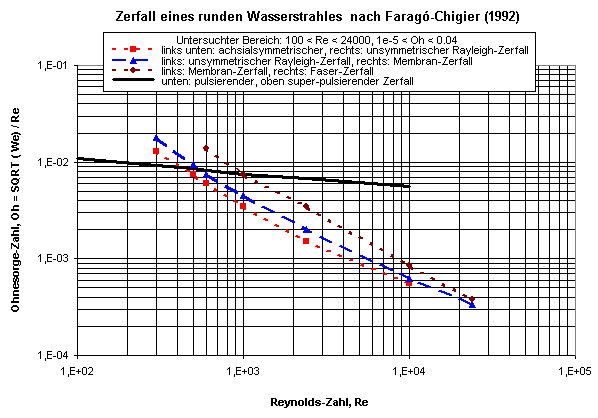
Faragó, Z. und Chigier, N.: Morphologycal Classification of Disintegration of Round Liquid Jets in a Coaxial Air Stream; Die Darstellung in Atomisation and Sprays, Vol. 2, pp. 137-157, 1992, zeigt die Zerfallsmodi in dem Reynolds-Weber-Diagramm
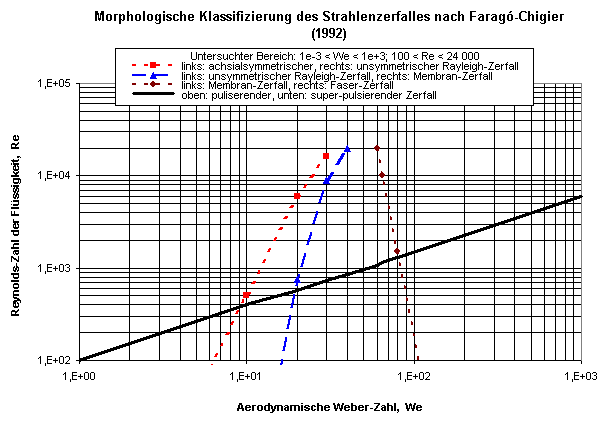
Faragó, Z. und Chigier, N.: Morphologycal Classification of Disintegration of Round Liquid Jets in a Coaxial Air Stream, Atomisation and Sprays, Vol. 2, pp. 137-157, 1992
Zeit und Längenskalen:
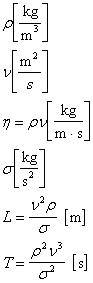
Wasser 20°C L=1.39e-8
m 
T=1.90e-10 s
100°C L=1.49e-9 m T=7.37e-12 s
Heizöl 50°C L=2.49e-7 m T=2.07e- 8 s
Ideal Jet Deformation without breakup and surface minimization:
 |
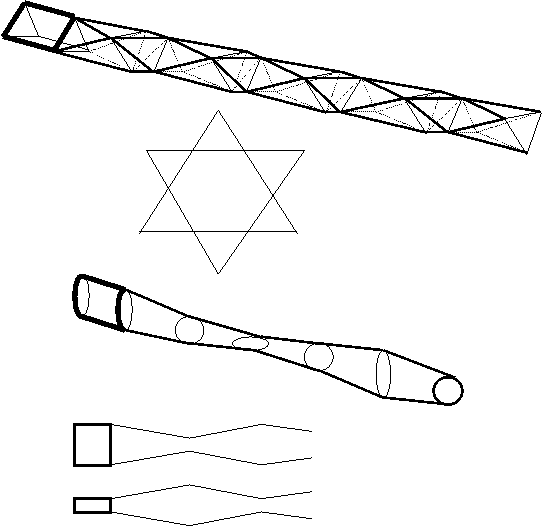