Musikalische Stimmungen gestern und heute –

Musical Temperaments yesterday and today

Hörbeispiele für alte Musik mit historischen Stimmungen

www.farago.info/hobby/stimmungen/StimmungenTonartencharakter.pptx

In dieser Arbeit werden fünfundzwanzig historische Stimmungen vorgestellt, mit deren Hilfe Liebhaber alter Musik alle Stücke vom 15. Jahrhundert bis zur Gegenwart in dem jeweils passenden Temperament spielen können. Die vorgestellten Stimmungen wurden mit einem Synthesizer (Korg X50) mit diversen Klängen für Piano, Orgel und Cembalo ausprobiert. Einige der alten Stimmungen sind beim ersten Hinhören gewöhnungsbedürftig, beim zweiten interessant, ab dem dritten wirken sie bereits wie eine Droge. Klingen „Magnificat-Fugen“ von Johann Pachelbel (1653-1706) im prätorianischen- oder im Werckmeister-Temperament (1691) besser? – Ausprobieren! Und wie hört sich „Der Wittembergische Galliart mit folgendem nachtantz“ (E. N. Ammerbach – 1583) in der E.-N.-Ammerbach-Stimmung (Leipzig, 1571) an? – Ausprobieren! Bereits gesagt: wie eine Droge!

Diese Studie entstand im Rahmen der akustischen Forschungen des Autoren Zoltán Faragó im DLR_School_Lab_Lampoldshausen des Deutschen Zentrums für Luft- und Raumfahrt, in Mai 2013.

Die authentische Wiedergabe historischer Musik mit leicht zu stimmenden Tasteninstrumenten (Spinett, Clavichord, Cembalo etc.) setzt eine der jeweiligen Musik entsprechende historische Stimmung voraus. Um den Stimm-Aufwand zu erleichtern, bieten einige Hersteller Stimmgeräte mit historischen Stimmungen an. Digitalpianos und Digitalorgeln haben oft eine Vielzahl historischer Stimmungen, die per Knopfdruck eingestellt werden können. Bei vielen Keyboards können auch eigene Stimmungen erstellt werden – die Möglichkeit hierzu heißt im Keyboard-Fachjargon „user scale tuning“. Im Internet sind Hunderte historischer Stimmungen zu finden, unter anderem bei folgenden Links:

http://www.schubiger-electronic.ch/deutsch/rtg4b2.htm [1]

http://www.instrument-tuner.com/temperaments_de.html [2]

http://home.arcor.de/wschmidts/german/start_d.html [3]

http://www.wolfgang-wiese.de/Historische%20Stimmungen-Schwebungen.pdf [4]

http://www.orgelbau-rohlf.de/themen/stimmungen/stimmungen.htm [5]

http://www.farago.info/hobby/stimmungen/Stimmtabellen.pdf [6]

Die für die jeweilige Komposition optimale Stimmung zu finden ist oft schwer. Die nachfolgenden Diagramme können die Auswahl erleichtern. Die X-Achse der gezeigten Diagramme stellt den Quintenzirkel dar, die Y-Achse die Abweichung des dritten und des fünften Tones der entsprechenden Dur- und Moll-Tonleiter von den natürlichen Terzen und Quinten. Die graphische Darstellung der Dur- und Moll-Dreiklänge und der Heptaton-Tonschritte verschiedener Stimmungen ist das Ergebnis eigener Berechnungen. Die Eingangsdaten der Berechnungen stammen größtenteils aus den Quellen [1] und [2].

Die optimale (schönste) Stimmung für ein musikalisches Werk ist die, die nur die Dur- und Moll-Dreiklänge als schöne Akkorde enthält, die im entsprechenden Werk tatsächlich vorkommen. Wenn in einem Musikstück nur wenige Harmonien auftreten, erklingen diese mit der optimalen Stimmung viel glanzvoller als mit der gleichschwebenden Temperierung oder mit einer Stimmung, die für Kompositionen mit einer Vielzahl harmonischer Variationen geschaffen wurde. Wenn eine Stimmung für viele Harmonien optimiert ist, sind die entsprechenden Dreiklänge weit weniger schön als mit einer Stimmung, die nur wenige Harmonien unterstützt. Kompositionen aus Renaissance und Frühbarock weisen relativ geringe harmonische Variationen auf – solche Werke klingen in gleichstufiger Stimmung nicht optimal. Die authentische Wiedergabe historischer Musik setzt eine der jeweiligen Musik entsprechende historische Stimmung voraus.

Definitionen

Die Töne der Dur-Tonleiter werden in dieser Arbeit mit den Termini do, re, mi, fa, so, la, ti, do‘

bezeichnet. Bei c-Dur ist c = do, bei d-Dur d = do usw.

fn: f (Hz) Frequenz des Tones n; fn/fm: Frequenzverhältnis des Tonintervalls m – n

Cent: f1/f2= 2^(1/1200) = 1,00057779 bzw. 1 Cent

Gleichschwebender Halbton: f1/f2 = 2^(1/12) = 1,0594631 bzw. 100 Cent

Halbton der reinen Stimmung: f1/f2 = 16/15 = 1.0666666⋅ bzw. 111,731 Cent

Kleiner Ganzton (rein): f1/f2 = 10 / 9 bzw. 182,404 Cent

Großer Ganzton (rein): f1/f2 =9/8 = 1,125 bzw. 203,91 Cent

Mollterz (kleine Terz): f1/f2 = 6/5 = 1,2 bzw. 315,641 Cent

Durterz (große Terz): f1/f2 = 5/4 = 1,25 bzw. 386,315 Cent

Quart: f1/f2 = 4/3 = 1,3333333⋅ bzw. 498,045 Cent

Quint: f1/f2 = 3/2 = 1,5 bzw. 701,955 Cent

Oktave: f1/f2 = 2 bzw. 1200 Cent

PK : Pythagoreisches Komma; Frequenzverhältnis von 12 Quinten zu 7 Oktaven,

PK = f1/f2 = (3/2)¹² / 2⁷ = 1,013643265 bzw. 23,46000224 Cent

WM: Werckmeister; WM = f1/f2 = PK ^(1/12) = 1,00112989 bzw. 1,955000186 Cent.

WM wird in der Literatur oft als 1/12 Komma bezeichnet.

SK: Syntonisches (Didymisches) Komma; Verhältnis zwischen dem großen und dem kleinem

Ganzton, SK = f1/f2 = (9/8) / (10/9) = 81/80 = 1,0125 bzw. 21,506 Cent

Sch: Schisma; Verhältnis zwischen dem pythagoreischen und dem didymischen Komma:

Sch = f1/f2 = 1, 00112915 bzw. 1,95372 Cent

Die Intervalle WM und Sch beschreiben den etwa gleichen Tonabstand; das Verhältnis WM/Sch hat

den Zahlenwert von f₁/f₂= 1,000000739 bzw. 0,00128 Cent.

Abweichung im Tonintervall zwischen zwei Tönen mit dem Frequenzverhälntis f1 und f2 in Cent:

ΔCent(f₁,f₂) = log(f₁/f₂)/log(2^1/1200) Gl. (1)

Berechnung der Tonhöhe f1 aus f2 und der Frequenzabweichung ΔC:

f₁ = f₂⋅ (2^1/1200) ^Δ^Cent(^f1,f2) Gl. (2)

SK + Sch = PK Gl. (3)

Die gleichstufige Stimmung

Bild 1a

Bild 1b

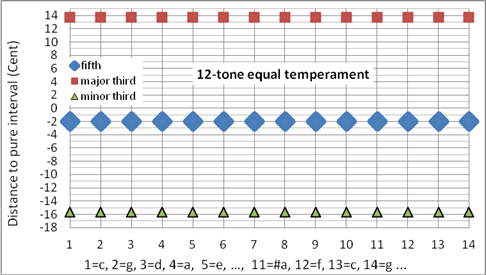
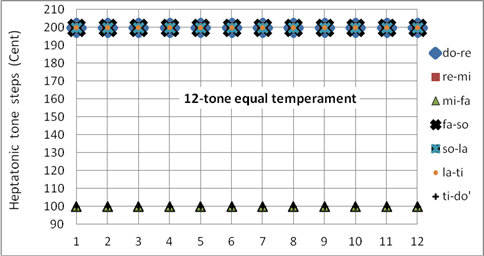
Der Ursprung der gleichstufigen Stimmung liegt in der Lautenmusik der Renaissance: Die Mensur der Renaissancelaute ergibt bei chromatischen Schritten eine Saitenverkürzung im Verhältnis 17/18, was ziemlich genau die gleichstufige Temperatur ergibt. Für Tasteninstrumente hat sich die gleichstufige Stimmung erst im 18. Jahrhundert durchgesetzt. Dabei wurden elf Quinten schwach verkleinert; Wenn die so entstandene zwölfte Quint genauso schwach verkleinert wie die anderen elf erschien, war die Stimmung befriedigend. Ab Ende des 19. Jahrhunderts wurde der Qualitätsanspruch höher: Die Quinten und Terzen sollten, wenn chromatisch aufwärts steigend gespielt, gleichstufig schnellere Schwebungen aufweisen. Nach diesem strengeren Maßstab gemessen, ist diese Temperatur erst ab Ende des 19. Jahrhunderts verbreitet [8] (pp. 10, 42,43). Aus diesem Grund passen die in Tabelle 4 gezeigten „nahezu-gleichstufigen-Stimmungen“ besser zur Musik des 19. Jahrhunderts als die wirkliche gleichstufige Temperatur.

Bei zwölfstufigen Musikinstrumenten gibt es keine Stimmung, die für alle Tonarten rein sind. Die meisten Stimmungen sind für einige Tonarten (auf Kosten anderer) optimiert. Bei allen nichtgleichstufigen Stimmungen gibt es klangliche Unterschiede zwischen den verschiedenen Tonarten. Die gleichstufige Stimmung ist ein Spezialfall, bei der alle Tonarten gleich klingen. Alle Halbton-Abstände betragen 100 Cent, alle Ganzton-Abstände 200. Alle Quint-Abstände sind 1 WM (ca. 2 Cent) zu eng, alle Dur-Terzen sind im Vergleich zur reinen Terz ca. 14 Cent zu hoch. Dies hat zu einer Veränderung der Hörgewohnheiten geführt: Einem Pianisten erscheint die reine Terz meist als zu eng. Bei der gleichstufigen Temperatur kann der für die alte Musik oft wichtige Charakterunterschied der Tonarten nicht wiedergegeben werden.

Sofern keine andere Stimmung angegeben, wird die gleichstufige Stimmung in annähernd allen digitalen Keyboards, so auch im Synthesizer Korg X50, als Standardstimmung angewandt.

Die pythagoreische Stimmung

Der griechische Gelehrte und Mönch Pythagoras von Samos unterstrich die Einfachheit und die Harmonie der Welt, indem er alles auf die Zahlen eins bis vier (und deren Kombinationen) zurückführte: In der Antike gibt es vier Himmelsrichtungen, vier Jahres- und vier Tageszeiten, vier Elemente und auch die Musik ist mit den Zahlen 1, 2, 3 und 4 (beziehungsweise deren Kombinationen) beschreibbar:

Grundton 1, Oktave 2, Quint 3/2, Quart 4/3,

Ganzton als Unterschied zwischen Quint und Quart (3/2)/(4/3) = 3 ²/2 ³ (203,9 Cent) und

Halbton als Unterschied zwischen Quart und zwei Ganztönen (4/3)/(( 3 ²/2 ³)⋅( 3 ²/2 ³)) = 256/243 (90,2 Cent).

Die ionische Tonleiter, aus der unsere heutige Durtonleiter hervorging, besteht aus

zwei Ganztönen + einem Halbton + drei Ganztönen + einem Halbton.

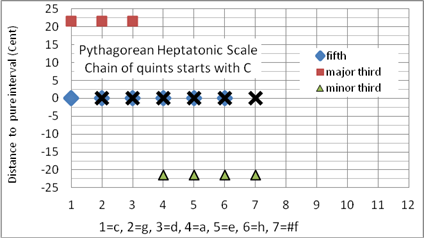
Die Quinten und Quarten sind rein, zum ersten Ton gibt es allerdings keine Quart und zum letzten keine Quint (siehe Bild 2). Zu den ersten drei Tönen der Quinten-Kette kann eine im Vergleich zur reinen großen Terz um das SK (siehe Definitionen) erhöhte Durterz, zu den letzten vier Tönen der Quinten-Kette eine um den gleichen Betrag herabgesenkte Mollterz zugeordnet werden.

Bild 2

Wird die reine Quinten-Kette (mit dem gebotenen Oktavieren) auf 13 Schritte erweitert, entstehen die in Bild 3 gezeigten Tonabstände: großer Ganzton (203,9 Cent), kleiner Ganzton (180,4Cent), ein großer Halbton (113,7 Cent): Tonabstände, die denen der reinen Stimmung ganz nahe kommen. Die Oktave do-do‘ ist um das PK zu groß, weshalb diese Stimmung in der Musik keine Anwendung findet (siehe Bild 3).

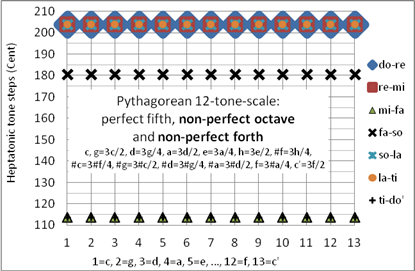Bild 3

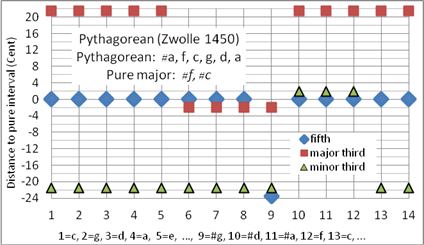
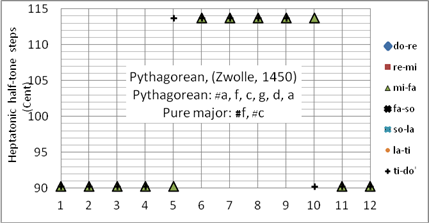
Die älteste Beschreibung der oktavreinen pythagoreischen Stimmung stammt von dem flämischen Arzt, Astronomen, Physiker, Orgelbauer und Organisten Henry Arnulf de Zwolle (1400-1466). Demnach werden die Quinten (mit dem gebotenen Oktavieren) elfmal rein gestimmt, der zwölfte Abstand ergibt sich von selbst – nämlich eine um das PK verminderte Quint #g-#d (Bild 4). Diese verminderte und etwas unangenehm klingende Quint wird oft als Wolfsquint bezeichnet.

Bild 4 a

Bild 4 b

Bild 4 c

Die von de Zwolle (1450) beschriebene Stimmung ergibt in #a-, f-, c-, g-, d- und a-Dur die pythagoreisch-heptatonische Tonleiter, in h-, #f- und #c-Dur die annähernd reine Durtonleiter. Die Zwolle-Stimmung wird im Synthesizer Korg X50 als pythagoreische Stimmung angewandt. Wird als Tonzentrum #f-Dur gewählt und das Musikstück in c-Dur gespielt, so erklingt es annähernd wie in der reinen Stimmung.

Die reine Stimmung

Die Schönheit der natürlichen oder reinen Stimmung wird durch keine andere Stimmungsart erreicht. Die natürliche Stimmung kann in der Regel nur für die Harmonisierung einer einzigen Tonart verwendet werden, sogar in dieser Tonart ist man Einschränkungen unterworfen. Die Tonleiter besteht aus Tonintervallen, deren Frequenzverhältnisse mit kleinen ganzen Zahlen beschreibbar sind. Die Tonhöhe der einzelnen Töne ist identisch mit einigen Obertönen des Grundtones. Die Tonleiter beinhaltet drei Intervalle: den großen, den kleinen Ganzton und den Halbton. Von den Ganzton-Intervallen do-re und re-mi ist abwechselnd ein Intervall groß und eines klein, das Intervall so-la ist immer klein, die Intervalle fa-so und ti-do‘ sind immer groß.

Intervall

Dur-Tonleiter

do-re

re-mi

mi-fa

fa-so

so-la

la-ti

ti-do‘

großer

(oder kleiner) Ganzton

kleiner

(oder großer)

Ganzton

Halbton

großer Ganzton

kleiner Ganzton

großer Ganzton

Halbton

Frequenzverhältnis

9/8

203,91 Cent

10/9

182,40 Cent

16/15

111,7Cent

9/8

203,91 Cent

10/9

182,4 Cent

9/8

203,9Cent

16/15

111,7Cent

Frequenzverhältnis zum Grundton

do-re

9/8

203,91 Cent

do-mi

5/4

386,32Cent

do-fa

4/3

498 Cent

do-so

3/2

702 Cent

do-la

5/3

884,4 Cent

do-ti

15/8

1088 Cent

do-do‘

2/1

1200 Cent

Intervall

Moll-Tonleiter

La-Ti

Ti-do

do-re

re-mi

mi-fa

fa-so

so-la

großer Ganzton

Halbton

großer

(oder kleiner) Ganzton

kleiner

(oder großer) Ganzton

Halbton

großer Ganzton

kleiner Ganzton

Frequenzverhältnis

9/8

203,9 Cent

16/15

111,7 Cent

9/8

203,91 Cent

10/9

182,40 Cent

16/15

111,7 Cent

9/8

203,9 Cent

10/9

182,40 Cent

Frequenzverhältnis zum Grundton

La-ti

9/8

203,9 Cent

La-do

6/5

315,6 Cent

La-re

4/3

498,05 Cent

La-mi

3/2

701,96 Cent

La-fa

8/5

813,7Cent

La-so

9/5

996,1Cent

La-la

2/1

1200 Cent

Tabelle 1: Frequenzverhältnisse der reinen Tonleiter

Die älteste Beschreibung einer reinen Stimmung stammt von Ramis de Pareja (Bologna 1482): Wenn die Wolfsquinte nicht um das PK, sondern lediglich um das SK verengt wird (siehe Definitionen, Gleichung (3)), entsteht eine reine Stimmung. Die zur Oktavreinheit fehlende Sch wird an einer anderen Stelle in den Quintzirkel eingebaut. Die Ramis-de-Pareja-Stimmung ergibt die natürliche Temperatur mit dem Tonzentrum f-Dur. Die reine Stimmung mit dem Tonzentrum in a-Dur wird von Martin Agricola (1539) beschrieben. Die Kirnberger-I-Stimmung (1766) ergibt die natürliche Stimmung mit dem Tonzentrum in c-Dur (siehe Tabellen 1 und 2).

Ramis de Pareja, Bologna 1482

Quint

-SK

-Sch

Durterz

SK-Sch

Tonleiter

rein

~Pyth.

rein

Martin Agricola, Wittenberg 1539

Quint

-SK

-Sch

Durterz

SK-Sch

Tonleiter

Pyth.

rein

Pyth.

Johann Philipp Kirnberger 1766, Kirnberger I

Quint

-SK

-Sch

Durterz

SK-Sch

Tonleiter

rein

Pyth.

Tabelle 2: SK- und Sch-Verteilung in den Stimmungen von de Pareja, Agricola und Kirnberger I

Eine Abweichung vom reinen Intervall um PK, SK oder SK-Sch ist deutlich hörbar und klingt unangenehm. Eine Abweichung um Sch ist hingegen kaum wahrnehmbar.

Die Stimmungen von R. de Pareja, Agricola und Kirnberger I sind rein für je eine Durtonleiter:

R. de Pareja für f-, Agricola für a- und Kirnberger I für c-Dur. Der Stimmungsvorgang ist sehr einfach. Dies kann am Beispiel der Kirnberger-I-Stimmung verdeutlicht werden: 1) der Ton d wird mit der Stimmgabel gestimmt; 2) die Töne g, c, f, #a, #d, #g, #c werden entlang der absteigenden Quintrichtung rein gestimmt;

3) die Intervalle f-a, c-e und g-h werden terzrein gestimmt; 4) der Ton #f wird so gestimmt, dass die Quint-Intervalle #f-#c und h-#f die gleiche Reibung aufweisen.

Die Bedeutung dieser Stimmungen bis Anfang des 16. Jahrhunderts wurde durch die klare und einfache Regel des Stimmungsvorganges ermöglicht. Jedoch ist die Harmonisierung bei dieser Stimmung wegen der Wolfsquint re-la eingeschränkt: Bald wurden neue Stimmungen entwickelt.

Bild 5 a

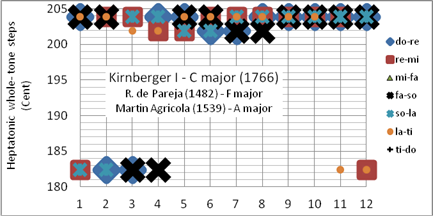Bild 5 b

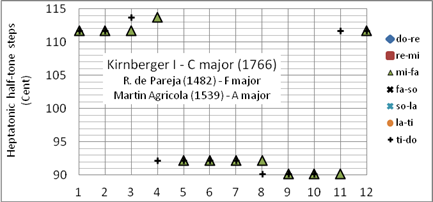Bild 5 c

Die in Bild 5 gezeigte Kirnberger-I-Stimmung weist drei reine Dur- (f-, c- und g-Dur) und drei reine Moll-Dreiklänge auf (e-, h- und #f-Moll), die c- Dur-Tonleiter ist rein.

Die Ramis-de-Pareja-Version (1482) ist graphisch nicht dargestellt. Nach de-Pariejas Aussage war sie zu seiner Zeit längst gebräuchlich. Diese Temperatur ist der erste Schritt von der pythagoreischen Stimmung weg in Richtung wohltemperiert.

Bild 6 a

Bild 6 b

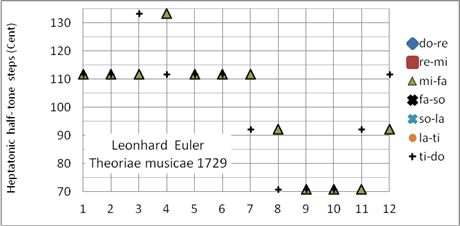Bild 6 c

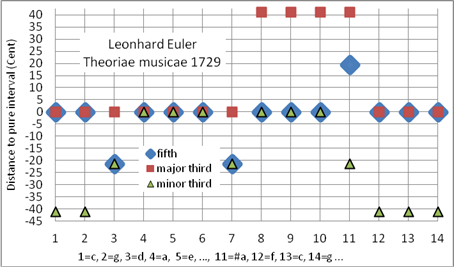
Leonhard Euler (1707 – 1783), einer der größten Mathematiker aller Zeiten, stellte in seinem Aufsatz Tentamen novae theoriae musicae [7] (erstellt 1729, veröffentlicht 1739) das eulersche Tonnetz und zugleich eine reine Stimmung vor, in der die Quintabstände d-a und #f-#c um das SK vermindert und #a-f um den Betrag SK-Sch erhöht wurden (Bild 6). Die Stimmung enthält vier reine Durtonleitern (c-, g-, e- und h-Dur), sechs reine Durdreiklänge (f-, c-, g-, a-, e und h-Dur) und sechs reine Molldreiklänge (a-, e-, h-, #c-, #g und #d-Moll). Die Durterzen der Töne #c, #g, #d und #a sind um 2⋅SK zu weit. Das eulersche Tonnetz wird oft als eine Art „musikalische Naturwissenschaft“ betrachtet. Es dient als Grundlage für die Konstruktion weiterer reiner Stimmungen. Programmiert als Korg User Scale 00 (pure major)

Bild 7a

Bild 7b

Bild 7c

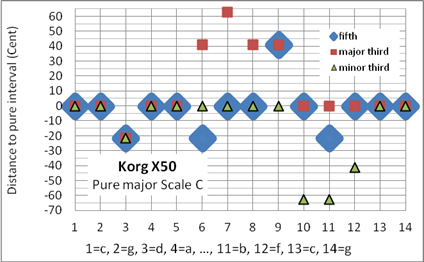
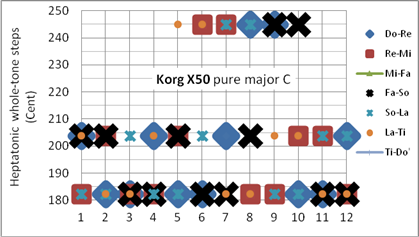
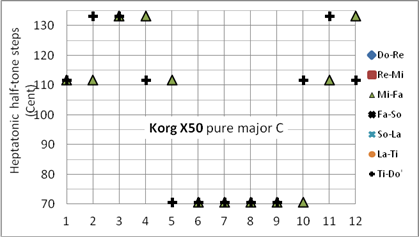
Um die Anzahl der Dreiklänge, die sowohl als Dur- als auch als Moll-Dreiklang rein sind, zu erhöhen, haben zahlreiche Musiktheoretiker jede vierte Quint des Quintenzirkels um ein SK vermindert und einen weiteren Quintabstand um den Betrag von 2⋅SK-Sch erweitert. Ein Beispiel hierzu ist die im Synthesizer Korg X50 angewandte „pure-major-scale“ mit verminderten Quinten für d-a, h-#f, #a-f und der entsprechenden Quint-Erweiterung für #g-#d, wie dargestellt in Bild 7 und Tabelle 3.

Der Vergleich der in Tabelle 3 dargestellten reinen Stimmungen zeigt, dass der Synthesizer Korg X50 die geringste Anzahl von reinen Tonleitern beinhaltet und gleichzeitig die größte Wolfsterz (#f-Dur, Abweichung 3⋅SK) aufweist. Hier liegt wahrscheinlich ein Programmierfehler vor, der möglicherweise auf einer Fehlinterpretation der J.-Mattheson-Stimmung beruht (vergleiche Quinten-Verschiebungen in Bildern 7a und 8a). Bei der Konstruktion der Stimmung „pure-major-scale“ im Korg X50 wird das im [7] beschriebene Prinzip verletzt. . Die Position „Quint“ in Spalte „#f“ ist identisch für die Stimmungen Euler, Marpurg, Schugk und Mattheson, die einzige Ausnahme bildet Korg X 50! Dies ist der Grund zum schlechten Abschneiden der Stimmung Korg X 50.

[7] Leonhard Euler: Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae. St. Petersburg 1739

	c	g	d	a	e	h	#f	#c	#g	#d		#a	f
*L. Euler 1729* reine Tonleiter: c-, g-, e-, und h-Dur (Bild 6)
Quint	0	0	*-SK*	0	0	0	*-SK*	0	0		0	SK	0
Durterz	0	0	0	0	0	0	0	2 ⋅SK	2 ⋅SK		2 ⋅SK	2 ⋅SK	0
Mollterz	-2⋅ SK	-2⋅ SK	*-SK*	0	0	0	*-SK*	0	0		0	*- SK*	-2⋅ SK
Tonleiter	rein	rein	-	-	rein	rein	-	-	-		-	-	-
*Rein Marpurg* reine Tonleiter: c- und g-Dur
Quint	0	0	*-SK*	0	0	0	*-SK*	0	2⋅ SK		0	*-SK*	0
Durterz	0	0	0	0	0	2 ⋅SK	2 ⋅SK	2 ⋅SK	2 ⋅SK		0	0	0
Mollterz	0	0	*-SK*	0	0	0	*-SK*	0	0		-2⋅ SK	-3 ⋅SK	-2⋅ SK
Tonleiter	rein	rein	-	-	-	-	-	-	-		-	-	-
*Schugk* reine Tonleiter: c-, g- und #d-Dur
Quint	0	0	*-SK*	0	0	0	*-SK*	2⋅ SK	0		0	*-SK*	0
Durterz	0	0	0	0	2 ⋅SK	2 ⋅SK	2 ⋅SK	2 ⋅SK	0		0	0	0
Mollterz	0	0	*-SK*	0	0	0	*-SK*	0	-2⋅ SK		-2⋅ SK	-3 ⋅SK	0
Tonleiter	rein	rein	-	-	-	-	-	-	-		rein	-	-
*J. Mattheson* 1681-1764 reine Tonleiter: c-, g- und e-Dur (Bild 8)
Quint	0	0	*-SK*	0	0	0	*-SK*	0	0		2⋅ SK	*-SK*	0
Durterz	0	0	0	0	0	0	2 ⋅SK	2 ⋅SK	2 ⋅SK		2 ⋅SK	0	0
Mollterz	-2⋅ SK	0	*-SK*	0	0	0	*-SK*	0	0		0	-3 ⋅SK	-2⋅ SK
Tonleiter	rein	rein	-	-	rein	-	-	-	-		-	-	-
*Korg* *X 50* reine Tonleiter: c-Dur (Bild 7)
Quint	0	0	*-SK*	0	0	*-SK*	0	0	2⋅ SK		0	*-SK*	0
Durterz	0	0	*-SK*	0	0	2 ⋅SK	3⋅SK	2 ⋅SK	2 ⋅SK		0	0	0
Mollterz	0	0	*-SK*	0	0	0	0	0	0		-3 ⋅SK	-3 ⋅SK	-2⋅ SK
Tonleiter	rein	-	-	-	-	-	-	-	-		-	-	-

Tabelle 3: Vergleich einiger reiner Stimmungen

Bei reinen Stimmungen ist die Tonleiter definitionsgemäß rein (im Sinne der Tonabstände nach Tabelle 1). Die Harmonisierung der einzelnen Töne ist, wenn lediglich die Töne der diatonischen Tonleiter verwendet werden, wie folgt möglich:

do → do-Dur, fa-Dur, la-Moll;

re → so-Dur;

mi → do-Dur, la-Moll, mi-Moll;

fa → fa-Dur;

so → do-Dur, so-Dur, mi-Moll;

la → fa-Dur, la-Moll;

ti → so-Dur, mi-Moll.

Bei der Harmonisierung der Töne re und fa ist keine Variation möglich, denn re-Moll ist nicht rein: Das Intervall re-fa ist in allen reinen Stimmungen um das SK kleiner als die reine Mollterz, bei Korg X50 ist zusätzlich das Intervall re-fi (#fa) um den gleichen Betrag (SK) kleiner als die reine Durterz. Die Variationsmöglichkeit bei der Harmonisierung verbessert sich, wenn eine Stimmung gleich zwei oder drei reine Tonleitern aufweist, wie beispielsweise in den Stimmungen Euler, Marpurg, Schugk und Mattheson (siehe Tabelle 3).

Bild 8a

Bild 8b

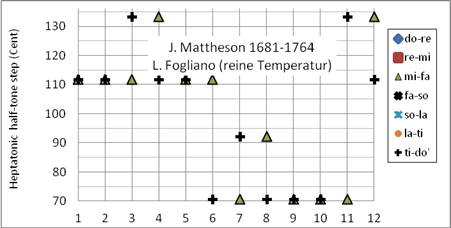Bild 8c

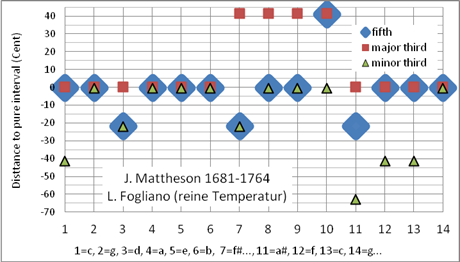
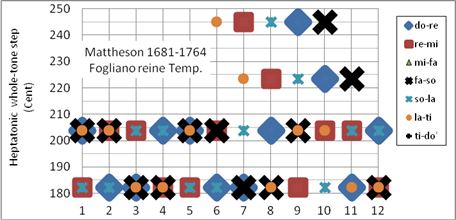
Bild 8 zeigt die von Johann Mattheson (1681-1764) vorgestellte reine Stimmung, die möglicherweise die Grundlage für die Korg-X50-Stimmung (pure-major-scale C) liefert. (Vergleiche die Position „Quint“ zwischen J. Mattheson und Korg X50 in Tabelle 2)

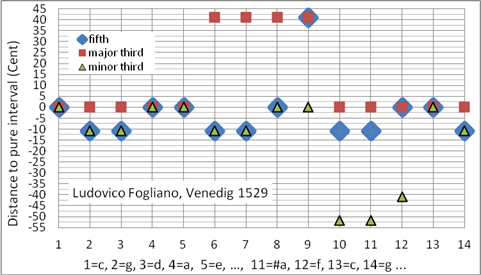
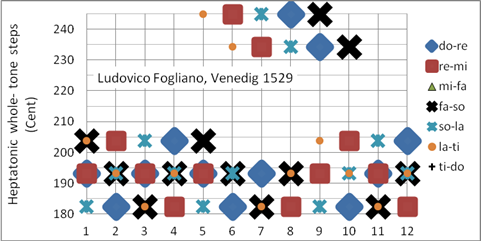
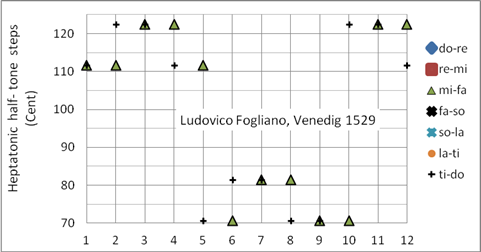
Ein Vorgänger der Mattheson-Stimmung mit dem Tonzentrum C (Bild 8) wurde bereits gut 200 Jahre vorher von Ludovico Fogliano, Venedig, 1529 mit dem Tonzentrum F beschrieben. Der Musiktheoretiker und Komponist Fogliano hat mehrere Stimmungen entwickelt (siehe auch Bild 9). Er war der Bruder des Organisten und Komponisten Giacomo Fogliano.

Bild 9 a

Bild 9b

Bild 9c

Ludovico Fogliano hat sich in seinen musiktheoretischen Arbeiten mit dem menschlichen Harmonieempfinden und mit Stimmungssystemen auseinandergesetzt. Die in Bild 9 gezeigte Stimmung lässt sich nicht eindeutig in eine Stimmungskategorie (wie rein, mitteltönig, wohltemperiert etc.) einordnen. Sie ist eine „reine“ Stimmung in dem Sinne, dass sie vier reine Dur- und ebenso viele reine Moll-Dreiklänge beinhaltet. Sie enthält aber nicht die in Tabelle 1 gezeigten Tonabstände der reinen Stimmung. Diese Stimmung ist sehr schön für die Tonarten bb – #### und ist vorwiegend für die Renaissancemusik geeignet. Programmiert als Korg User Scale 01 (pure major)

Historische Stimmungen des Synthesizers Korg X50

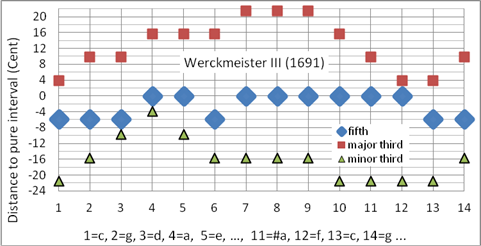Bild 10 a

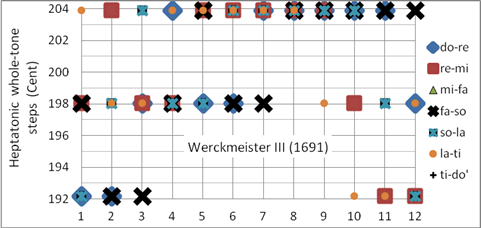Bild 10 b

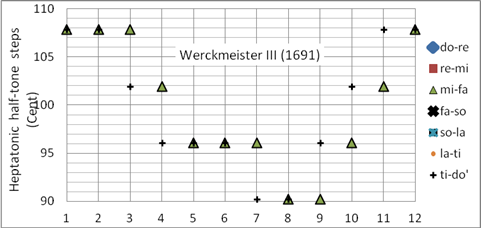Bild 10 c

Andreas Werckmeister veröffentlichte in seiner Studie „Musikalische Temperatur“ (1691) mehrere Stimmungsentwürfe (Werckmeister III, IV, V, VI), die er den in seiner Zeit üblichen Stimmungen (Werckmeister I und II) gegenüberstellte. Werckmeister III ist die meistverbreitete Werckmeister-Stimmung, die im Synthesizer Korg X50 einfach als Werckmeister bezeichnet wird. Sie wird in der Barockmusik sowohl für Orgel- als auch für Cembalo-Stimmung angewandt. Sie ist eine stark ungleichstufige wohltemperierte Stimmung. Gut geeignet für Tastenmusik des 18. Jahrhunderts.

Bild 11 a

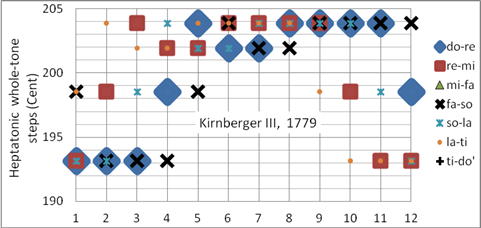Bild 11 b

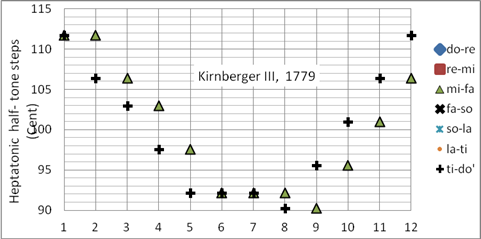Bild 11 c

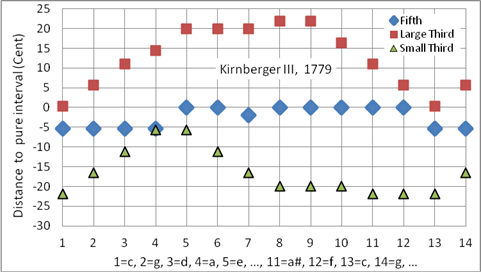
Kirnberger III ist die meistverbreitete Kirnberger-Stimmung, sie wird im Synthesizer Korg X50 als Kirnberger bezeichnet. Ihre beachtliche Verbreitung verdankt sie ihrer Ausgewogenheit und der Tatsache, dass sie – wie alle Kirnberger-Temperaturen – sehr leicht zu stimmen ist [12]:

1) c‘ und c werden mit Hilfe eines anderen Musikinstruments gestimmt;

2) entlang des Quintenzirkels (in Rückwärtsrichtung, d.h. c‘-f, f‘-#a usw.) werden die Intervalle bis einschließlich #g‘-#c‘ quintenrein gestimmt;

3) das Intervall c – e‘ wird rein (d.h. schwebungsfrei) gestimmt;

4) die Intervalle e‘-h‘ und h-#f‘ werden quintenrein gestimmt;

5) die verbleibenden Töne g, d und a werden so gestimmt, dass c‘-g‘, g-d‘ , d‘-a‘ und a-e‘ die gleiche Reibung aufweisen (e‘ ist bereits gestimmt nach 3)).

Die Kirnberger III-Stimmung ist ideal für das Cembalo des 18. Und 19. Jahrhunderts, als Orgelstimmung aber weniger geeignet.

Mitteltönige Stimmungen

Die mitteltönigen Stimmungen haben in einem begrenzten Tonart-Bereich (maximal 8 Tonarten) annähernd reine Terzen, die restlichen Tonarten weisen besonders unreine Terzen auf. Im Tonzentrum verschwindet der Charakter-Unterschied zwischen den Tonarten. Sie sind eine wichtige Stimmung in der Renaissance und im Barock und sind besonders für Orgel und Cembalo bis heute gebräuchlich. Die Bezeichnung „mitteltönig“ bedeutet, dass statt des großen und des kleinen Ganztons der reinen Stimmung hier ein mittlerer Ganzton verwirklicht wird. Die ersten mitteltönigen Stimmungen stammen aus dem Ende des 15. Jahrhunderts, die Blütezeit dieser Stimmung liegt im 16. und 17. Jahrhundert. Die erste Andeutung einer mitteltönigen Stimmung stammt von Franchinus Gaffurius (1451 – 1522, porträtiert von Leonardo da Vinci, Portrait eines Musikers). Gaffurius beschreibt die mitteltönige Stimmung als „bereits gebräuchlich“. Sie wird oft als prätorianische Temperatur bezeichnet.

Bild 12 a

Bild 12 b

Bild 12 c

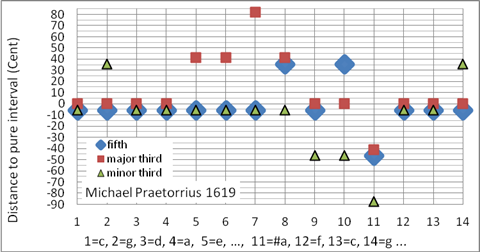
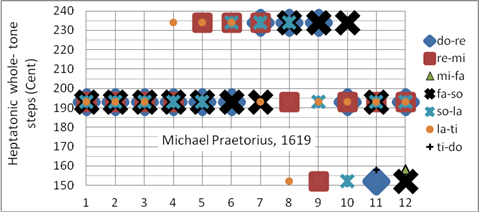
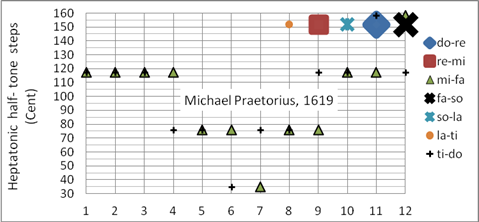
Die Praetorius-Stimmung ist eine mitteltönige Stimmung für die Tonarten c-, g- und d-Dur. Die restlichen Tonarten weisen nicht-tolerable Wolfstöne auf. Diese Stimmung war vermutlich bereits Ende des 15. Jahrhunderts gebräuchlich, Praetorius beschreibt sie als gängige Praxis [13]. Programmiert als Korg User Scale 02 (mitteltönig)

Bild 13 a

Bild 13 b

Bild 13 c

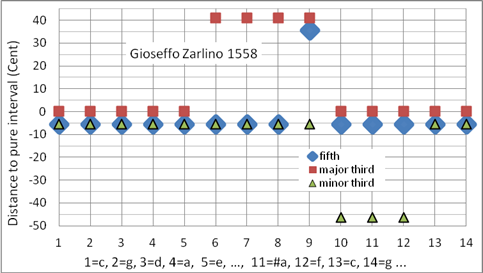
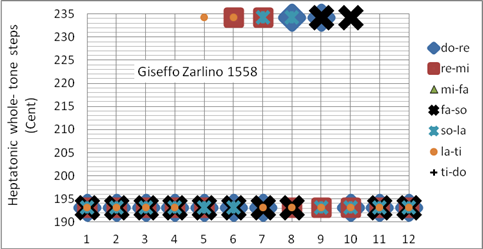
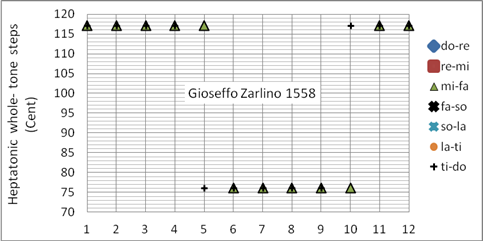
Die Zarlino-Stimmung ermöglicht das Spielen in den Tonarten bb – ###. Ab dem vierten # und dem dritten b treten übergroße Wolfstöne auf. Zarlino war Kapellenmeister im Markusdom (Venedig) und wird von vielen als Vater der modernen Musiktheorie bezeichnet, der bereits 1588 einen theoretischen Ansatz der gleichstufigen Temperatur aufstellt. Die in Bild 13 gezeigte Zarlino-Stimmung ist ideal für die Musik des 16. und 17. Jahrhunderts. Die unspielbaren Tonarten, in denen Wolfstöne auftreten, sind im 16. und 17. Jahrhundert nicht gebräuchlich. Sie ist eine sogenannte ¼-Komma Stimmung: die Verengung der Quinten beträgt SK/4, was zu reinen Durterzen führt. Interessanterweise ist die Reinheit der Terz im 16. und 17. Jahrhundert wichtiger als diejenige der Quinte. Dies ist im 18. Jahrhundert nicht mehr der Fall (siehe Silbermann-Sorge Stimmung). Programmiert als Korg User Scale 03 (mitteltönig)

Bild 14 a

Bild 14 b

Bild 14 c

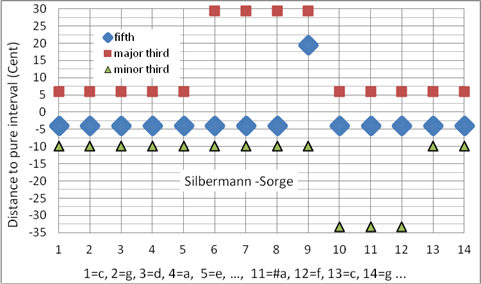
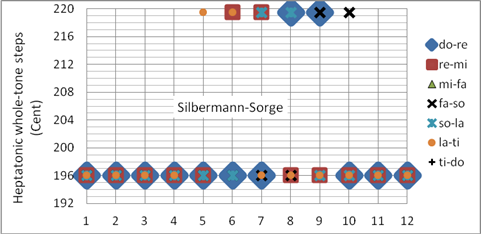
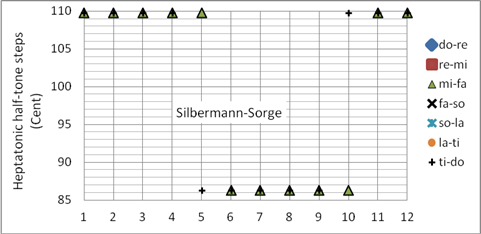
Die Silbermann-Sorge-Temperatur ist nach dem Orgelbauer Gottfried Silbermann (1683-1753) und dem Musiktheoretiker Georg Andreas Sorge (1703-1778) benannt. Diese Stimmung wird in vielen Barock-Orgeln angewandt. Die Quintverengung beträgt elfmal 2WM. Die Dur- und Moll-Dreiklänge in den Tonarten bb – ### sind eine Nuance weniger schön, die Wolfstöne der restlichen Tonarten sind wiederum weniger schlecht als die der Zarlino-Stimmung (Bild 13). Die Unreinheit der Quinten und der Terzen ist in dieser Stimmung etwa gleich groß. Programmiert als Korg User Scale 04 (mitteltönig)

Bild 15 a

Bild 15 b

Bild 15 c

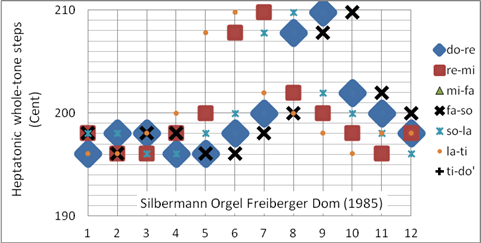
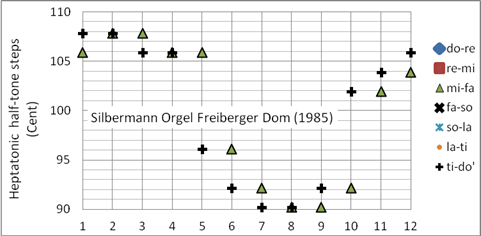
Bei der Restaurierung historischer Barockorgeln wird oft eine verfeinerte mitteltönige Stimmung angewandt, welche das Spielen in allen Tonarten ermöglicht. Die Dur- und Mollterzen im Tonzentrum haben eine größere Abweichung von den reinen Intervallen als bei der Silbermann-Sorge Temperatur. Bild 15 zeigt die Stimmung der großen Silbermann Orgel im Freiberger Dom nach der Restaurierung 1985. (Im Freiberger Dom gibt es zwei Silbermann-Orgeln, die große und die kleine.) Bei der Restaurierung obiger Silbermann-Orgel wurde eine quasi-mitteltönige Stimmung mit erkennbarer Tendenz zur wohltemperierten verwirklicht. Programmiert als Korg User Scale 05 (mitteltönig)

Ansätze zur wohltemperierten Stimmung

Heute verstehen wir unter wohltemperierter Stimmung ungleichstufige musikalische Temperaturen, die das Spielen in allen Tonarten ermöglichen. Was „wohl“ klingt und was nicht, ist jedoch teilweise von unseren Hörgewohnheiten abhängig, die sich in den vergangenen Jahrhunderten geändert haben. Die Stimmungen Ramis de Pareja und Martin Agricola (siehe Tabelle 2) waren in der Renaissance möglicherweise in allen Tonarten spielbar, wenn auch der Terminus „wohltemperiert“ erst durch Andreas Werckmeister 1681 entstanden ist. Heute werden die Stimmungen Ramis de Pareja oder Agricola nicht als wohltemperiert bezeichnet. Bilder 16 bis 20 zeigen den Weg, der zu den wohltemperierten Stimmungen führt.

Bild 16 a

Bild 16 b

Bild 16 c

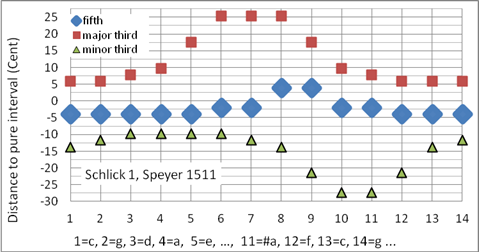
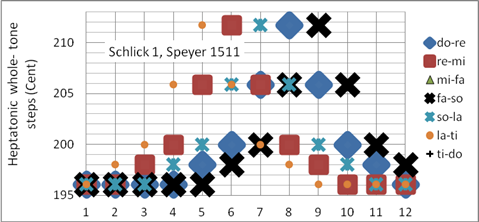
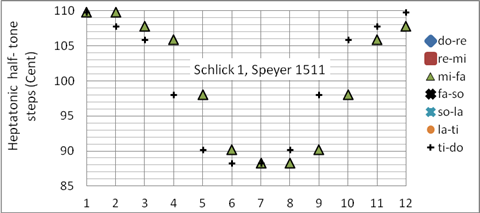
Die Schlick 1 Stimmung (Speyer 1511) kann als Vorgänger der späteren wohltemperierten Stimmungen angesehen werden. Schlick war Organist, Lautenist und der erste Musiktheoretiker, der eine nicht-mitteltönige, ungleichschwebende, in seiner Zeit in allen Tonarten spielbare Stimmung beschrieben hat. Die Ähnlichkeit dieser Temperatur zur mitteltönig-wohltemperierten Stimmung der Silbermann Orgel im Freiberger Dom (Bild 15) ist unverkennbar: Schlick war seiner Zeit um viele Jahrhunderte voraus! Arnold Schlick beschreibt im „Spiegel der Orgelmacher und Organisten“ (1511) zwei weitere (mitteltönige) Stimmungen, bekannt als Schlick-2- und Schlick-3-Temperament. Programmiert als Korg User Scale 06

Bild 17 a

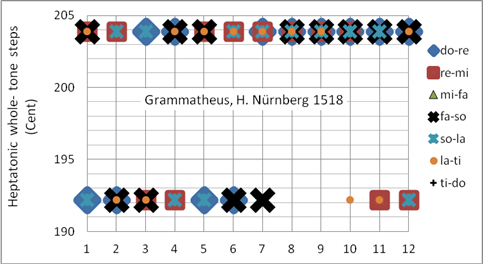Bild 17 b

Bild 17 c

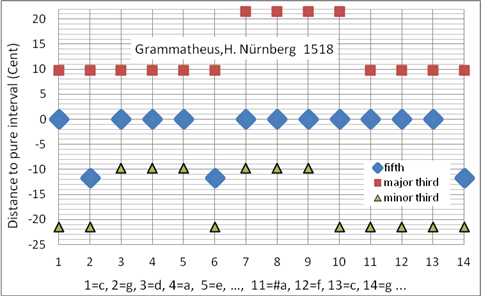
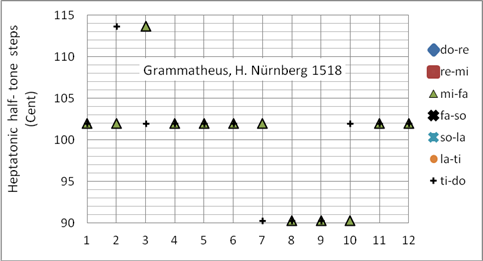
Grammatheus Henricus (Heinrich Schreyber) war Mathematiker und Vorbote der gleichschwebenden Temperatur. Er hat zwei Quinten um PK/2 verkleinert; es gibt verschiedene Interpretationen, welche zwei. Kirnberger verfeinerte diese Stimmung, indem er die zwei Quinten um SK/2 und eine weitere Quinte um Sch verkleinerte (Kirnberger II). Auch bei Kirnberger II gibt es verschiedene Interpretationen. Die Grammatheus-Stimmung wird bei Cembalo für Musik des 16. Jahrhunderts oft angewandt. Programmiert als Korg User Scale 07

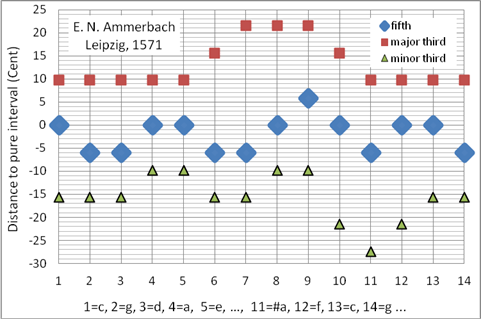Bild 18 a

Bild 18 b

Bild 18 c

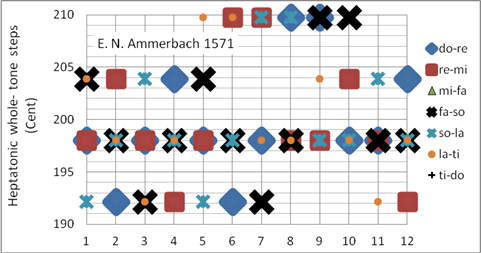
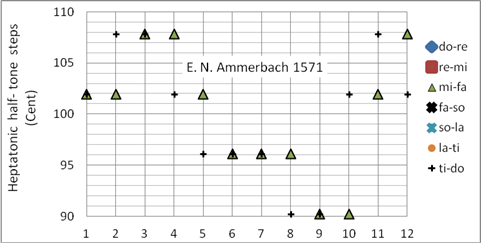
Die Durdreiklänge der Ammerbach-Stimmung sind in den Tonarten b – #### schöner als die der gleichstufigen und in keiner schlechter als die der pythagoreischen Stimmung. Elias N. Ammerbach war 1561 – 1595 Organist der Thomaskirche. In Deutschland pulizierte er die ersten Orgel-Tabulaturen. Die von ihm veröffentlichten Werke (Orgel- und Virginal-Literatur) klingen mit der Ammerbach-Stimmung authentisch. Programmiert als Korg User Scale 08

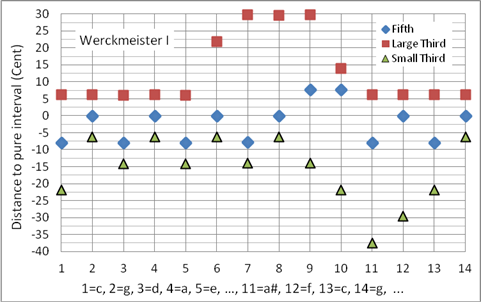Bild 19 a

Bild 19 b

Bild 19 c

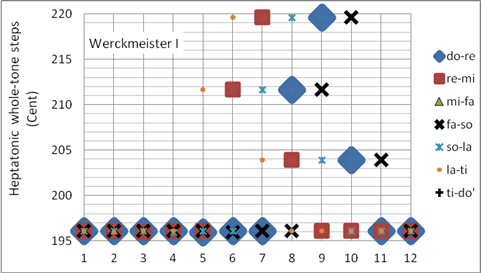
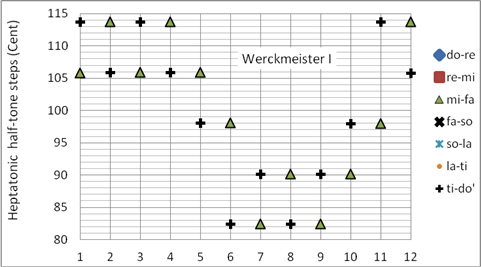
Andreas Werckmeister stellt seine Simmungen (Werckmeister III bis IV) den in seiner Zeit üblichen Temperaturen gegenüber (Werckmeister I und II). Die Werckmeister I (und II) Stimmung wurde zwar von Werckmeister beschrieben, aber nicht von ihm konstruiert. Die Werckmeister I Stimmung (1697) ist eine mitteltönige Temperatur, sie ist zur Zeit der Veröffentlichung bereits gängige Praxis. Programmiert als Korg User Scale 09

Bild 20 a

Bild 20 b

Bild 20c

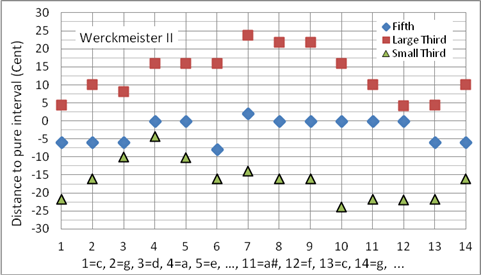
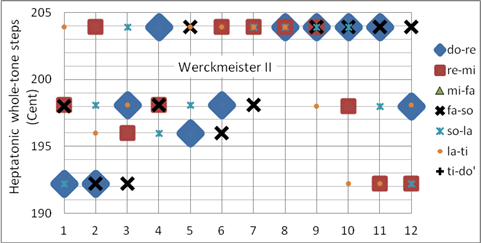
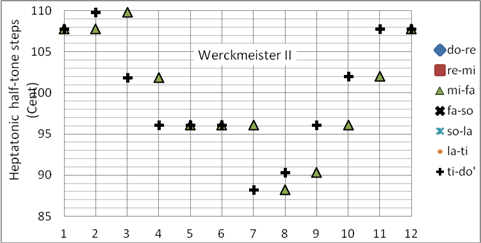
Die als Werckmeister II bezeichnete Stimmung ist so unausgewogen, dass sie nur als Vorstufe der wohltemperierten Stimmung angesehen wird. Die Durterz in #f-Dur ist schärfer als die der pythagoreischen, und die Halbton-Intervalle mi – fa und ti – do‘ in d- bzw. #f-Dur sind viel zu groß. Die #c-Dur-Tonleiter ist annähernd pythagoreisch. Nach heutigen Hörgewohnheiten sind #f-, #c- und #g-Dur-Dreiklänge sehr scharf. Die #f-#a-Terz ist um ein PK zu hoch. Sie ist zur Zeit der Veröffentlichung (1697) bereits gängige Praxis. Programmiert als Korg User Scale 10

Wohltemperierte Stimmung

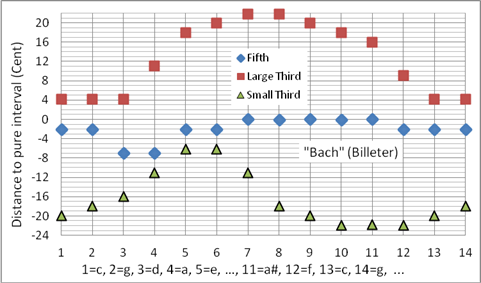
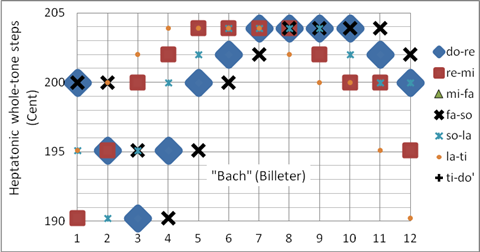
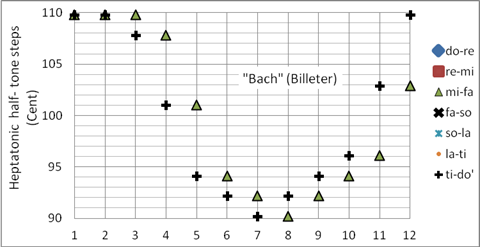
Als wohltemperierte Stimmungen gelten die Temperaturen, deren schlechteste Terz von der reinen Terz nicht mehr als um das SK abweicht. Die wohltemperierten Stimmungen ermöglichen das Klavierspiel in allen Tonarten. Der Trend geht dabei zu immer gleichstufigeren Temperaturen. Im 17. und 18. Jahrhundert waren die wohltemperierten Stimmungen um einiges ungleichstufiger als 100 Jahre später. Johann Sebastian Bachs Das Wohltemperierte Klavier verdeutlicht die charakterlichen Unterschiede der verschiedenen Tonarten seiner Klavierstimmung. Wie J. S. Bach sein Clavichord gestimmt hat, ist nicht bekannt: Hierzu gibt es eine Vielzahl von Rekonstruktionen mit verschiedenen Ergebnissen. Bild 21 zeigt ein Beispiel, die sogenannte „Bach“ – Stimmung nach Billeter.

Bild 21 a

Bild 21 b

Bild 21 c

Bernhard Billeter (Pianist, Organist und Musiktheoretiker) schuf einen wichtigen Beitrag zum Stimmen von Tasteninstrumenten. („Anweisungen zum Stimmen von Tasteninstrumenten in verschiedenen Temperaturen“ , Merseburger Verlag, 1979). Billeters Interpretation der „Bach“-Stimmung zeigt den reinen Toncharakter in f- und c-Dur und ist nahezu pythagoreisch in #f- und #c-Dur. Keine der in dieser Arbeit vorgestellten wohltemperierten Temperaturen zeigt den Charakterunterschied der Tonarten f-, c-, g-, d- und a-Dur so deutlich wie Billeters „Bach-Stimmung“. Programmiert als Korg User Scale 11

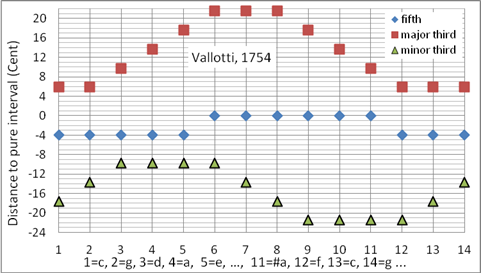Bild 22 a

Bild 22 b

Bild 22 c

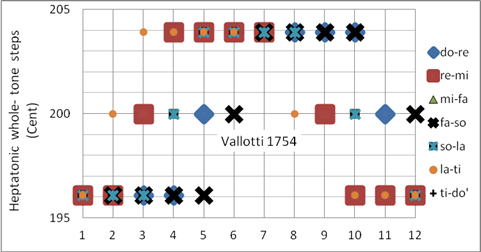
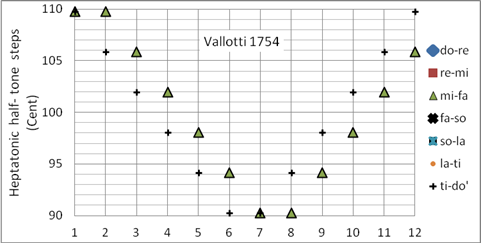
Die Vallotti-Stimmung ist einer der meistverbreiteten Stimmungen der historischen Aufführungspraxis. Während bei Billeters-Bach-Stimmung der schöne c-Dur-Dreiklang mit einer (im unteren Tetrachord) reinen Tonleiter aufwartet, ist in der Vallotti-Stimmung die c-Dur-Tonleiter mit mitteltönigen Ganztönen verwirklicht. Die #f-Dur-Tonleiter ist pythagoreisch. Die Großterzen sind fast rein in f-, c- und g-Dur und pythagoreisch in den entfernten Tonarten. Sie ist fast identisch mit der Stimmung von Young Thomas (1800). Programmiert als Korg User Scale 12

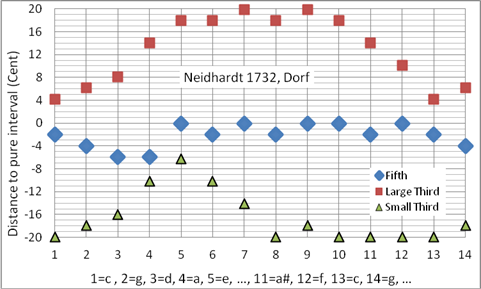Bild 23 a

Bild 23 b

Bild 23 c

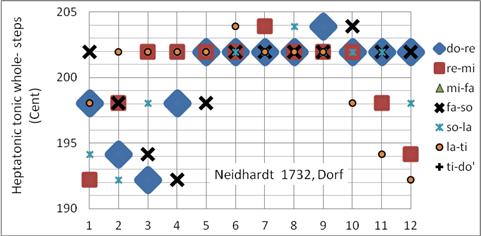
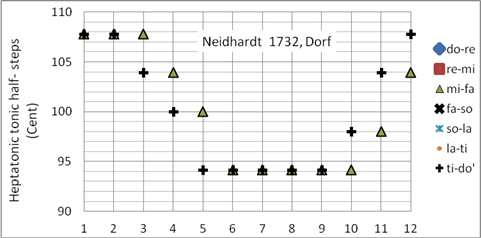
Johann Georg Neidhardt war Organist, Komponist und Musiktheoretiker. Er war ein Vorkämpfer der gleichstufigen Stimmung. Seine Stimmung Für ein Dorf ist für Dorforganisten gedacht, die Tonarten mit wenigen Vorzeichen bevorzugten. Sie ist ideal für Tonarten b – ##, jedoch in allen anderen Tonarten spielbar. Neidhardt beschreibt 6 Stimmungen: „Dorf“, „kleine Stadt“, „große Stadt“, Neidhardt 1, Neidhardt 2 und Neidhardt 3. Die Stimmung „Dorf“ weist die größte Abweichung zur gleichstufigen Stimmung auf, doch gerade diese Stimmung zeigt den größten Charakterunterschied bei den Tonarten f-, c-, g- und d-Dur auf. Programmiert als Korg User Scale 13

Bild 24 a

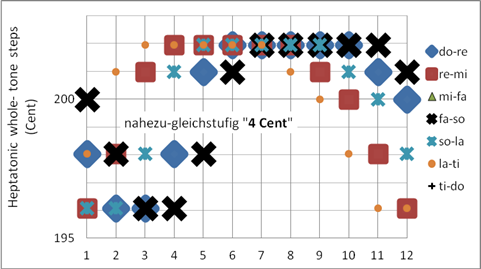Bild 24 b

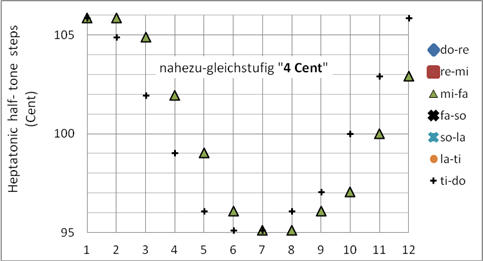Bild 24 c

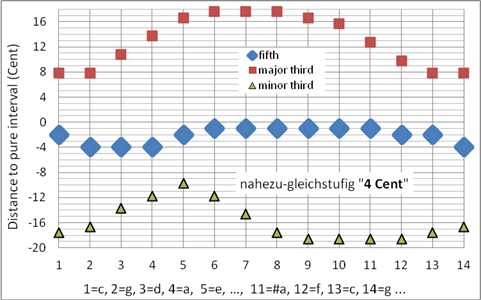
In der nahezu-gleichstufigen Stimmung „4 Cent“ beträgt die maximale Tonabweichung von der gleichstufigen Temperatur weniger als 4 Cent (2Sch). Der Charakterunterschied der Tonarten ist im Tonzentrum (c-Dur) deutlich größer als fern vom Zentrum. Programmiert als Korg User Scale 14

Bild 25 a

Bild 25 b

Bild 25 c

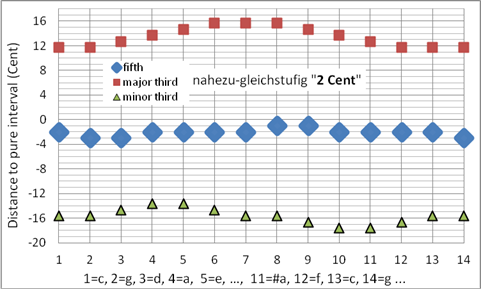
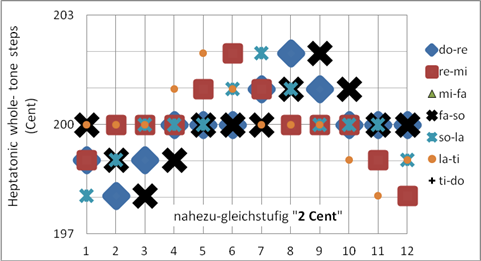
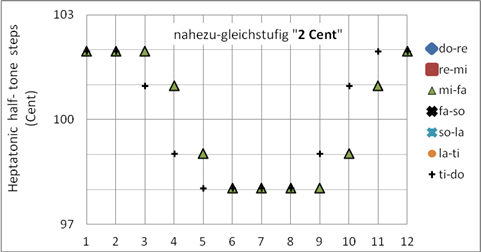
Die nahezu-gleichstufige Stimmung „2 Cent“ ist im Tonzentrum nicht so schön wie die Variante

„4 Cent“, fern vom Tonzentrum ist sie hingegen schöner. Die maximale Abweichung von der gleichstufigen Stimmung beträgt 1Sch. Programmiert als Korg User Scale 15

Tabelle der hier vorgestellten und mit Korg X50 demonstrierten historischen Stimmungen

Korg X50 vorkonfigurierte Stimmungen
			Bild	Bemerkung
	Equal temperament	Gleichstufig	1		19.Jahrhundert-Gegenwart
	Van Zwolle 1450	Pythagoreisch	4	1	14-16. Jahrhundert
	Fogliano (?)	Natürlich	7	2	Fogliano, Venedig 1529
	Werckmeister (III), 1691	Wohltemperiert	10	3	17.-19. Jahrhundert
	Kirnberger (III), 1769	Wohltemperiert	11	3	18.-19. Jahrhundert
1 c einstellen: Pythagoreisch; ------ #f einstellen, c spielen: ~ Natürlich
2 möglicherweise eine Fehlinterpretation der Fogliano-Mattheson-Stimmung
3 ta (bti) - do‘ = 204 Cent
Korg X50 User Scale
00	Euler, 1729	Natürlich	6	1,2*	18.Jahrhundert-Gegenwart
01	Fogliano, 1528	~Natürlich	9	2	16.-17. Jahrhundert
02	Praetorius, 1619	Mitteltönig	12	6	15.-16.Jahrhundert
03	Zarlino, 1558	Mitteltönig	13		16.-18. Jahrhundert
04	Silbermann, Sorge	Mitteltönig	14		18.Jahrhundert-Gegenwart
05	Freiberger Dom (1985)	~Mitteltönig	15		Tendenz zu wohltemperiert [13]
06	Schlick 1, 1511	~Wohltemperiert	16	6	16.-17. Jahrhundert
07	Grammatheus 1518	~Wohltemperiert	17		16.-17. Jahrhundert
08	Ammerbach, 1571	~Wohltemperiert	18		16.-17. Jahrhundert
09	Werckmeister I, 1691	~Mitteltönig	19	6	17.-18. Jahrhundert
10	Werckmeister II, 1691	~Wohltemperiert	20	2,6	17.-18. Jahrhundert
11	„Bach“ (Billeter) 1722 (1979)	Wohltemperiert	21	2	18.Jahrhundert
12	Vallotti 1754	Wohltemperiert	22	5	18.-19. Jahrhundert
13	Neidhardt „Dorf“ 1732	Wohltemperiert	23	2	18.-19 Jahrhundert
14	Nahezu-gleichstufig (4 Cent)	Wohltemperiert	24	3,7	19. Jahrhundert-Gegenwart
15	Nahezu-gleichstufig (2 Cent)	Wohltemperiert	25	4,7	19. Jahrhundert-Gegenwart
~ das Zeichen „~“ bedeutet: annähernd; quasi; mint Tendenz zu; mit Abstrich etc.
1 Beim Tonzentrum e c -Dur gut harmonisierbar
2 Der Tonabstand (verminderter Sept) – Grundton = 204 Cent 2* = 225 Cent
3 max. 4 Cent Abweichung von der gleichstufigen Stimmung
4 max. 2 Cent Abweichung von der gleichstufigen Stimmung
5 c-DurTonleiter mitteltönig
6 zur Zeit der Veröffentlichung bereits „gängige Praxis“
7 siehe Kommentare zur gleichstufigen Stimmung, 1. Absatz nach Bild 1b

Tabelle 4: Verzeichnis 21 wichtiger musikalischen Temperaturen

Weiterführende Literatur (Kurzauszug)

[ 8] Robert Schröter: Die Stimmung von Tasteninstrumenten

http://www.robertschroeter.de/diplom.pdf

[ 9] William A. Sethares: Tuning, Timbre, Spectrum, Scale; Springer

[ 9] Bernhard Billeter: Anweisung zum Stimmen von Tasteninstrumenten; Merseburger

[10] Bálint Dobozi: Vergleich verschiedener wohltemperierter Stimmungen

http://www.fres.ch/bd/content/music/bach.html

[11] Jan van Biezen: Stemmingen, speciaal bij toetsinstrumenten

http://www.janvanbiezen.nl/Stemmingen.pdf

[12] Carey Beebe Harpsichords; Technical Library, Temperaments

http://www.hpschd.nu/index.html?nav/nav4.html&t/welcome .html&http://www.hpschd.nu/tech/tmp/faq.html

[13] Kristian Wegscheider: Mit reinem Herzen – reine Terzen

http://www.wegscheider.eu/img/Juergen.pdf